-
추정치 구하기
-
predict() 사용
야구 데이터 추정하기
-
홈런(HR)에 대한 루타(TB) 회귀분석 하기
# 데이터 로드 df_kbo <- read.csv('r-ggagi-data/example_kbo2015.csv')head(df_kbo, 3)ranking team AVG G PA AB R H X2B X3B ⋯ IBB HBP SO GDP SLG OBP OPS MH RISP PH.BA <int> <chr> <dbl> <int> <int> <int> <int> <int> <int> <int> ⋯ <int> <int> <int> <int> <dbl> <dbl> <dbl> <int> <dbl> <dbl> 1 1 삼성 0.300 102 4091 3553 634 1066 188 19 ⋯ 15 47 650 78 0.471 0.374 0.845 101 0.300 0.216 2 2 넥센 0.300 102 4151 3620 658 1085 227 12 ⋯ 13 61 815 79 0.498 0.374 0.872 100 0.294 0.268 3 3 두산 0.291 99 3950 3410 570 991 176 16 ⋯ 17 66 544 95 0.438 0.368 0.806 98 0.284 0.262 # 회귀모델 구하기 Lm <- lm(HR~TB, data = df_kbo)Lm # y = -109.2696 + 0.1441x (1.44개의 홈런 / 10개의 안타)Call: lm(formula = HR ~ TB, data = df_kbo) Coefficients: (Intercept) TB -109.2696 0.1441# 회귀모델 검증 # Multiple R-squared : 0.9039 # p-value : 2.423e-05 # Pr(>|t|) 2.42e-05 summary(Lm)Call: lm(formula = HR ~ TB, data = df_kbo) Residuals: Min 1Q Median 3Q Max -7.991 -4.702 -3.498 4.471 11.884 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -109.26964 24.92619 -4.384 0.00234 ** TB 0.14411 0.01661 8.677 2.42e-05 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 7.963 on 8 degrees of freedom Multiple R-squared: 0.9039, Adjusted R-squared: 0.8919 F-statistic: 75.28 on 1 and 8 DF, p-value: 2.423e-05# 회귀모델에 값을 넣어 추정치 구하기 p <- predict(Lm)p- 1
- 131.825268238313
- 2
- 150.2712623156
- 3
- 105.885589067127
- 4
- 117.990772680347
- 5
- 118.278991337805
- 6
- 88.3042509622124
- 7
- 85.7102830450938
- 8
- 91.3305468655174
- 9
- 86.286720360009
- 10
- 83.1163151279752
# 두 값 비교하기 c(df_kbo$HR[1], p[1]) c(df_kbo$HR[2], p[2])- 1
- 127
- 1
- 131.825268238313
- 1
- 155
- 2
- 150.2712623156
# 모든 값 비교하기 Com <- data.frame(team = df_kbo$team, HR = df_kbo$HR, fittedHR = round(p), fittedHR = p) Comteam HR fittedHR fittedHR.1 <chr> <int> <dbl> <dbl> 1 삼성 127 132 131.82527 2 넥센 155 150 150.27126 3 두산 98 106 105.88559 4 NC 110 118 117.99077 5 롯데 130 118 118.27899 6 SK 92 88 88.30425 7 한화 82 86 85.71028 8 kt 87 91 91.33055 9 LG 83 86 86.28672 10 KIA 95 83 83.11632 루타가 1600일 때, 홈런의 갯수는?
# 같은 변수명 data.frame 으로 만들어야 함 newTeam <- data.frame(TB = 1600) predict(Lm, newTeam)1: 121.30528724111
# 삼성 df_kbo[1,]$TB1673
mtcars 데이터로 예측하기
-
연비(mpg) 종속변수(y), 차체 무게를 독립변수(x)로 회귀모델 구하기
df <- mtcars head(df, 3)mpg cyl disp hp drat wt qsec vs am gear carb <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1 str(df)'data.frame': 32 obs. of 11 variables: $ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ... $ cyl : num 6 6 4 6 8 6 8 4 4 6 ... $ disp: num 160 160 108 258 360 ... $ hp : num 110 110 93 110 175 105 245 62 95 123 ... $ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ... $ wt : num 2.62 2.88 2.32 3.21 3.44 ... $ qsec: num 16.5 17 18.6 19.4 17 ... $ vs : num 0 0 1 1 0 1 0 1 1 1 ... $ am : num 1 1 1 0 0 0 0 0 0 0 ... $ gear: num 4 4 4 3 3 3 3 4 4 4 ... $ carb: num 4 4 1 1 2 1 4 2 2 4 ...# 회귀모델 구하기 Lm <- lm(mpg~wt, data=df)Lm # 1ton 늘때마다 연비 5만큼 낮아짐Call: lm(formula = mpg ~ wt, data = df) Coefficients: (Intercept) wt 37.285 -5.344# 회귀모델 검증 # R-squared : 0.7528 # p-value : 0.0000000001294 (x값이 0이 될 확률) options(scipen = 999) summary(Lm)Call: lm(formula = mpg ~ wt, data = df) Residuals: Min 1Q Median 3Q Max -4.5432 -2.3647 -0.1252 1.4096 6.8727 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 37.2851 1.8776 19.858 < 0.0000000000000002 *** wt -5.3445 0.5591 -9.559 0.000000000129 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.046 on 30 degrees of freedom Multiple R-squared: 0.7528, Adjusted R-squared: 0.7446 F-statistic: 91.38 on 1 and 30 DF, p-value: 0.0000000001294# 추정치 구하기 p <- predict(Lm) p- Mazda RX4
- 23.2826106468086
- Mazda RX4 Wag
- 21.9197703957643
- Datsun 710
- 24.8859521186254
- Hornet 4 Drive
- 20.1026500610386
- Hornet Sportabout
- 18.900143957176
- Valiant
- 18.7932545257216
- Duster 360
- 18.2053626527221
- Merc 240D
- 20.2362618503567
- Merc 230
- 20.4500407132656
- Merc 280
- 18.900143957176
- Merc 280C
- 18.900143957176
- Merc 450SE
- 15.5331268663607
- Merc 450SL
- 17.3502472010864
- Merc 450SLC
- 17.0830236224503
- Cadillac Fleetwood
- 9.22665041054798
- Lincoln Continental
- 8.29671235689423
- Chrysler Imperial
- 8.71892561113932
- Fiat 128
- 25.5272887073521
- Honda Civic
- 28.6538045773949
- Toyota Corolla
- 27.4780208313959
- Toyota Corona
- 24.1110037405806
- Dodge Challenger
- 18.4725862313582
- AMC Javelin
- 18.9268663150396
- Camaro Z28
- 16.762355328087
- Pontiac Firebird
- 16.7356329702233
- Fiat X1-9
- 26.9435736741236
- Porsche 914-2
- 25.8479570017155
- Lotus Europa
- 29.1989406778126
- Ford Pantera L
- 20.3431512818111
- Ferrari Dino
- 22.4809399109002
- Maserati Bora
- 18.2053626527221
- Volvo 142E
- 22.427495195173
# 두 값 비교 data.frame(mpg=df$mpg, fittedMPG=p)mpg fittedMPG <dbl> <dbl> Mazda RX4 21.0 23.282611 Mazda RX4 Wag 21.0 21.919770 Datsun 710 22.8 24.885952 Hornet 4 Drive 21.4 20.102650 Hornet Sportabout 18.7 18.900144 Valiant 18.1 18.793255 Duster 360 14.3 18.205363 Merc 240D 24.4 20.236262 Merc 230 22.8 20.450041 Merc 280 19.2 18.900144 Merc 280C 17.8 18.900144 Merc 450SE 16.4 15.533127 Merc 450SL 17.3 17.350247 Merc 450SLC 15.2 17.083024 Cadillac Fleetwood 10.4 9.226650 Lincoln Continental 10.4 8.296712 Chrysler Imperial 14.7 8.718926 Fiat 128 32.4 25.527289 Honda Civic 30.4 28.653805 Toyota Corolla 33.9 27.478021 Toyota Corona 21.5 24.111004 Dodge Challenger 15.5 18.472586 AMC Javelin 15.2 18.926866 Camaro Z28 13.3 16.762355 Pontiac Firebird 19.2 16.735633 Fiat X1-9 27.3 26.943574 Porsche 914-2 26.0 25.847957 Lotus Europa 30.4 29.198941 Ford Pantera L 15.8 20.343151 Ferrari Dino 19.7 22.480940 Maserati Bora 15.0 18.205363 Volvo 142E 21.4 22.427495 # 차가 6톤일 때 연비 추정 NewCar <- data.frame(wt=6) predict(Lm, newdata = NewCar)1: 5.21829673100597
# 차가 400Kg일 때 연비 추정 NewCar <- data.frame(wt=0.4) predict(Lm, newdata = NewCar)1: 35.147337538253
diamonds 데이터로 캐럿에 따른 가격 예측하기
library(ggplot2)Warning message: "package 'ggplot2' was built under R version 4.0.2"df <- diamonds head(df, 3)carat cut color clarity depth table price x y z <dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl> 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31 str(df)tibble [53,940 x 10] (S3: tbl_df/tbl/data.frame) $ carat : num [1:53940] 0.23 0.21 0.23 0.29 0.31 0.24 0.24 0.26 0.22 0.23 ... $ cut : Ord.factor w/ 5 levels "Fair"<"Good"<..: 5 4 2 4 2 3 3 3 1 3 ... $ color : Ord.factor w/ 7 levels "D"<"E"<"F"<"G"<..: 2 2 2 6 7 7 6 5 2 5 ... $ clarity: Ord.factor w/ 8 levels "I1"<"SI2"<"SI1"<..: 2 3 5 4 2 6 7 3 4 5 ... $ depth : num [1:53940] 61.5 59.8 56.9 62.4 63.3 62.8 62.3 61.9 65.1 59.4 ... $ table : num [1:53940] 55 61 65 58 58 57 57 55 61 61 ... $ price : int [1:53940] 326 326 327 334 335 336 336 337 337 338 ... $ x : num [1:53940] 3.95 3.89 4.05 4.2 4.34 3.94 3.95 4.07 3.87 4 ... $ y : num [1:53940] 3.98 3.84 4.07 4.23 4.35 3.96 3.98 4.11 3.78 4.05 ... $ z : num [1:53940] 2.43 2.31 2.31 2.63 2.75 2.48 2.47 2.53 2.49 2.39 ...# 회귀모델 구하기 - 캐럿에 따른 가격 Lm <- lm(price~carat, data = df) Lm # 1캐럿이 올라가면 7756달러 올라감Call: lm(formula = price ~ carat, data = df) Coefficients: (Intercept) carat -2256 7756# 회귀 모델 검증 # Multiple R-squared : 0.8493 # p-value : < 0.00000000000000022 # Pr(>|t|) 0.00000000000000022 < 0.05 (0 이될 확률 낮음) options(scipen = 999) summary(Lm)Call: lm(formula = price ~ carat, data = df) Residuals: Min 1Q Median 3Q Max -18585.3 -804.8 -18.9 537.4 12731.7 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -2256.36 13.06 -172.8 <0.0000000000000002 *** carat 7756.43 14.07 551.4 <0.0000000000000002 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 1549 on 53938 degrees of freedom Multiple R-squared: 0.8493, Adjusted R-squared: 0.8493 F-statistic: 3.041e+05 on 1 and 53938 DF, p-value: < 0.00000000000000022# 10 캐럿 일 때, 가격 예측 NewDiamond <- data.frame(carat=c(10, 20))predict(Lm, newdata = NewDiamond)- 1
- 75307.895599639
- 2
- 152872.151779323
예측값 신뢰구간으로 나타내기
-
추정값을 x가 2일때 30이다 => x가 2일때 28~32이다
-
통계학은 항상 점추정보다 구간추정을 더 신뢰
-
예측구간 : 예측값의 신뢰구간
데이터의 신뢰구간을 그래프로 나타내기
library(ggplot2)df <- diamonds# 표본 추출 Sample <- diamonds[sample(nrow(df), 100), ] head(Sample)carat cut color clarity depth table price x y z <dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl> 1.14 Very Good H SI2 63.3 57 4615 6.60 6.63 4.19 1.23 Premium E SI1 59.2 62 7274 7.05 7.00 4.16 0.72 Ideal H VVS1 60.8 58 3180 5.77 5.80 3.52 1.11 Ideal H VS2 64.0 58 5632 6.52 6.46 4.16 0.30 Good H VS1 63.4 53 526 4.25 4.30 2.71 0.30 Ideal G VVS2 62.4 57 665 4.27 4.29 2.67 # 시각화 g1 <- ggplot(Sample, aes(x = carat, y=price, colour=color)) + geom_point() g1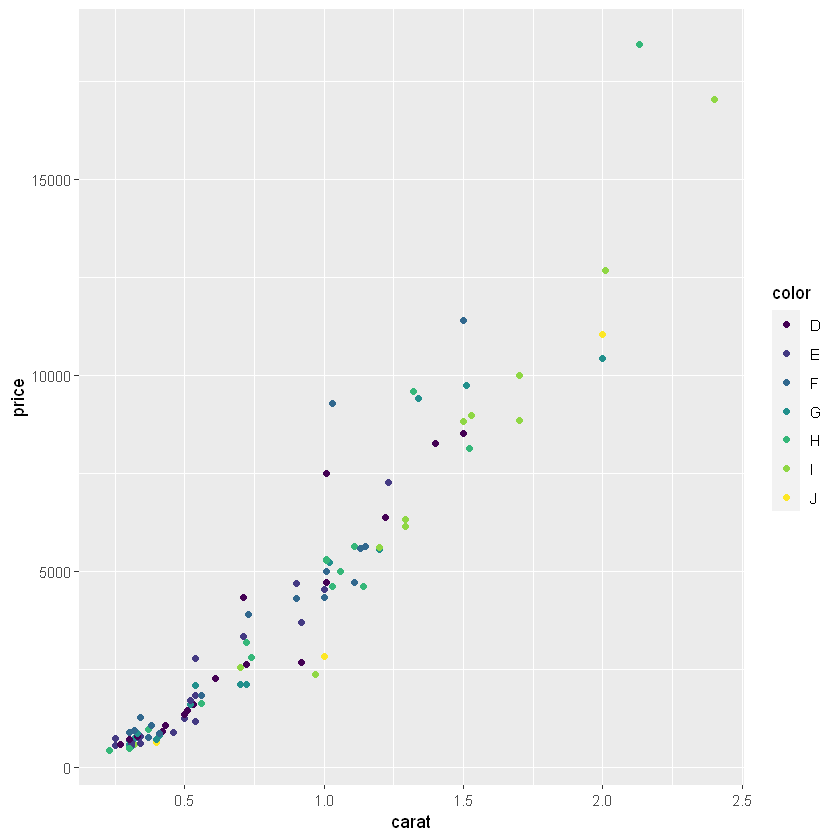
g2 <- ggplot(Sample, aes(x=carat, y=price)) + geom_point(aes(colour=color)) g2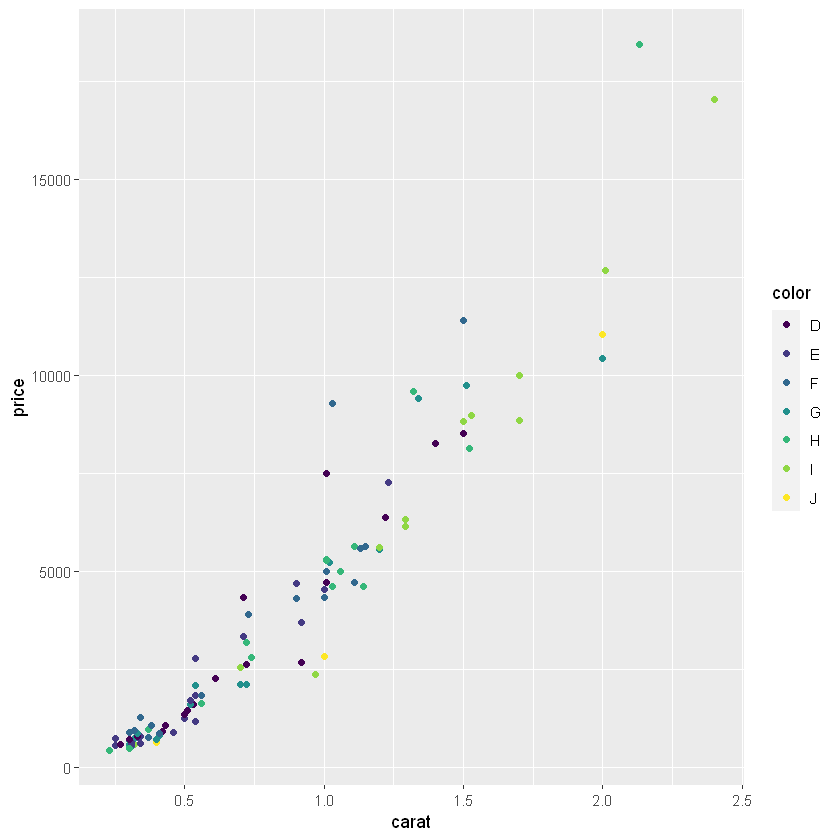
colour 속성으로 그룹별 회귀모델을 나타낼 수 있음
-
ggplot() 넣으면 그룹별
-
geom_point() 하나만 표시
# color 그룹별 회귀모델 g1 + geom_smooth(method = 'lm')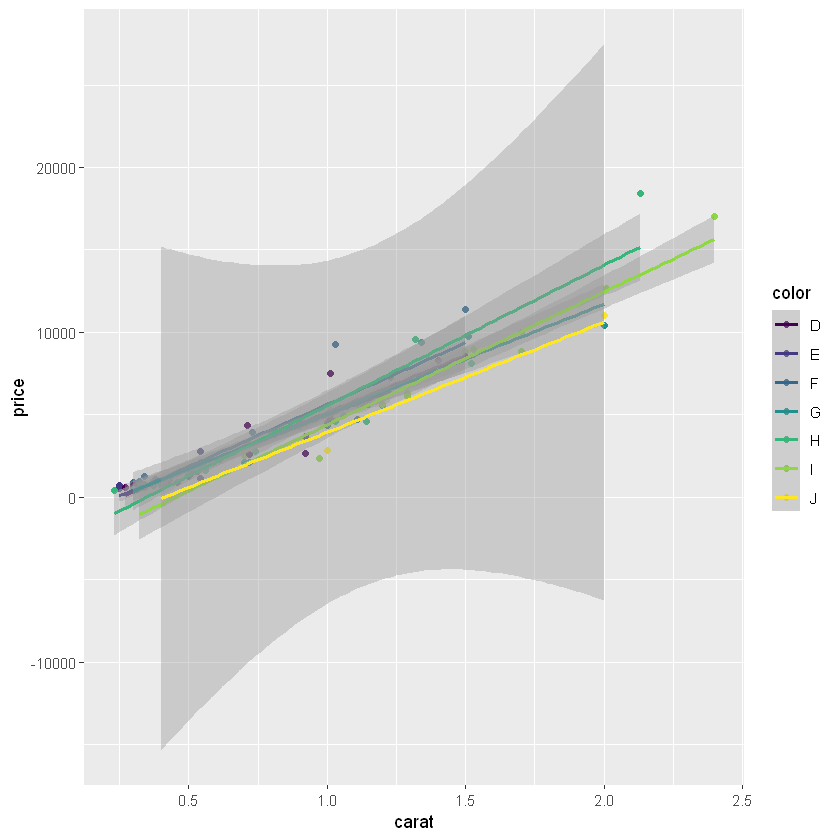
# color 그룹별 회귀모델 g2 + geom_smooth(method = 'lm')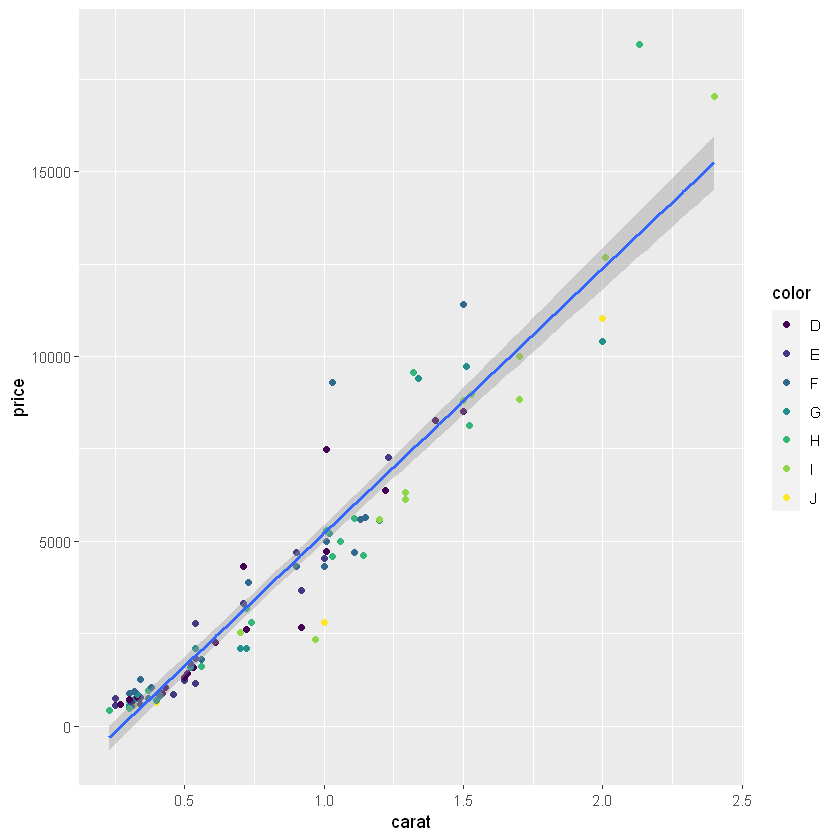
# 회귀모델 구하기 - 정확한 값으로 예측구간 나타내기 Lm <- lm(price~carat, data=Sample) LmCall: lm(formula = price ~ carat, data = Sample) Coefficients: (Intercept) carat -1960 7167# confidence : 평균신뢰구간, prediction 예측구간 p <- predict(Lm, interval = 'confidence', level = 0.95) head(p)fit lwr upr 1 6210.3498 5953.1074 6467.592 2 6855.3964 6575.1028 7135.690 3 3200.1325 2979.7940 3420.471 4 5995.3343 5744.8967 6245.772 5 189.9152 -121.7496 501.580 6 189.9152 -121.7496 501.580 다중선형 회귀분석에서 변수 선택법
전진선택법(forward selection)
-
기준 통계치를 가장 많이 개선시키는 변수를 차례로 추가하는 방법
후진제거법(backward elimination)
-
기준 통계치에 가장 도움이 되지 않는 변수를 하나씩 제거하는 방법
단계적 방법(stepwise selection)
-
모든 변수가 포함된 모델에서 기준 통계치에 도움되지 않는 변수를 삭제
-
모델에 빠진 변수중 통계치를 개선시키는 변수를 추가하는 방법
-
변수의 추가 또는 삭제를 반복
회귀모델에서 변수를 선택하는 판단 기준
-
AIC(아케이케 통계량) => R step()
-
BIC(슈바르츠 통계량) => leaps 패키지의 redsubset()
-
Cp(멜로우스 통계량)
-
세 통계량이 작을 수록 좋다.
다중공선성(Multicolinearity)
-
모형의 일부 예측변수가 다른 예측변수와 상관되어 있을 때 발생하는 조건
-
중대한 다중공선성은 회귀계수의 분산을 증가시켜 불안정하고 해석하기 어렵게 만들기 때문에 문제
-
R에서는 vif 함수를 이용해 VIF값을 구할 수 있으며, 보통 VIF값이 4가 넘으면 다중공선성이 존재한다고 봄
R에서 확인 하기
단계적 방법(stepwise selection)
df <- mtcarsLm <- lm(mpg~., data=df) LmCall: lm(formula = mpg ~ ., data = df) Coefficients: (Intercept) cyl disp hp drat wt 12.30337 -0.11144 0.01334 -0.02148 0.78711 -3.71530 qsec vs am gear carb 0.82104 0.31776 2.52023 0.65541 -0.19942step()
# step() - AIC 값 확인(작은 값) direction : 'both', 'backword', 'forward' # 각 단계의 + 는 탈락된 변수 df_step <- step(Lm, direction = 'both')Start: AIC=70.9 mpg ~ cyl + disp + hp + drat + wt + qsec + vs + am + gear + carb Df Sum of Sq RSS AIC - cyl 1 0.0799 147.57 68.915 - vs 1 0.1601 147.66 68.932 - carb 1 0.4067 147.90 68.986 - gear 1 1.3531 148.85 69.190 - drat 1 1.6270 149.12 69.249 - disp 1 3.9167 151.41 69.736 - hp 1 6.8399 154.33 70.348 - qsec 1 8.8641 156.36 70.765 <none> 147.49 70.898 - am 1 10.5467 158.04 71.108 - wt 1 27.0144 174.51 74.280 Step: AIC=68.92 mpg ~ disp + hp + drat + wt + qsec + vs + am + gear + carb Df Sum of Sq RSS AIC - vs 1 0.2685 147.84 66.973 - carb 1 0.5201 148.09 67.028 - gear 1 1.8211 149.40 67.308 - drat 1 1.9826 149.56 67.342 - disp 1 3.9009 151.47 67.750 - hp 1 7.3632 154.94 68.473 <none> 147.57 68.915 - qsec 1 10.0933 157.67 69.032 - am 1 11.8359 159.41 69.384 + cyl 1 0.0799 147.49 70.898 - wt 1 27.0280 174.60 72.297 Step: AIC=66.97 mpg ~ disp + hp + drat + wt + qsec + am + gear + carb Df Sum of Sq RSS AIC - carb 1 0.6855 148.53 65.121 - gear 1 2.1437 149.99 65.434 - drat 1 2.2139 150.06 65.449 - disp 1 3.6467 151.49 65.753 - hp 1 7.1060 154.95 66.475 <none> 147.84 66.973 - am 1 11.5694 159.41 67.384 - qsec 1 15.6830 163.53 68.200 + vs 1 0.2685 147.57 68.915 + cyl 1 0.1883 147.66 68.932 - wt 1 27.3799 175.22 70.410 Step: AIC=65.12 mpg ~ disp + hp + drat + wt + qsec + am + gear Df Sum of Sq RSS AIC - gear 1 1.565 150.09 63.457 - drat 1 1.932 150.46 63.535 <none> 148.53 65.121 - disp 1 10.110 158.64 65.229 - am 1 12.323 160.85 65.672 - hp 1 14.826 163.35 66.166 + carb 1 0.685 147.84 66.973 + vs 1 0.434 148.09 67.028 + cyl 1 0.414 148.11 67.032 - qsec 1 26.408 174.94 68.358 - wt 1 69.127 217.66 75.350 Step: AIC=63.46 mpg ~ disp + hp + drat + wt + qsec + am Df Sum of Sq RSS AIC - drat 1 3.345 153.44 62.162 - disp 1 8.545 158.64 63.229 <none> 150.09 63.457 - hp 1 13.285 163.38 64.171 + gear 1 1.565 148.53 65.121 + cyl 1 1.003 149.09 65.242 + vs 1 0.645 149.45 65.319 + carb 1 0.107 149.99 65.434 - am 1 20.036 170.13 65.466 - qsec 1 25.574 175.67 66.491 - wt 1 67.572 217.66 73.351 Step: AIC=62.16 mpg ~ disp + hp + wt + qsec + am Df Sum of Sq RSS AIC - disp 1 6.629 160.07 61.515 <none> 153.44 62.162 - hp 1 12.572 166.01 62.682 + drat 1 3.345 150.09 63.457 + gear 1 2.977 150.46 63.535 + cyl 1 2.447 150.99 63.648 + vs 1 1.121 152.32 63.927 + carb 1 0.011 153.43 64.160 - qsec 1 26.470 179.91 65.255 - am 1 32.198 185.63 66.258 - wt 1 69.043 222.48 72.051 Step: AIC=61.52 mpg ~ hp + wt + qsec + am Df Sum of Sq RSS AIC - hp 1 9.219 169.29 61.307 <none> 160.07 61.515 + disp 1 6.629 153.44 62.162 + carb 1 3.227 156.84 62.864 + drat 1 1.428 158.64 63.229 - qsec 1 20.225 180.29 63.323 + cyl 1 0.249 159.82 63.465 + vs 1 0.249 159.82 63.466 + gear 1 0.171 159.90 63.481 - am 1 25.993 186.06 64.331 - wt 1 78.494 238.56 72.284 Step: AIC=61.31 mpg ~ wt + qsec + am Df Sum of Sq RSS AIC <none> 169.29 61.307 + hp 1 9.219 160.07 61.515 + carb 1 8.036 161.25 61.751 + disp 1 3.276 166.01 62.682 + cyl 1 1.501 167.78 63.022 + drat 1 1.400 167.89 63.042 + gear 1 0.123 169.16 63.284 + vs 1 0.000 169.29 63.307 - am 1 26.178 195.46 63.908 - qsec 1 109.034 278.32 75.217 - wt 1 183.347 352.63 82.790# 최종 회귀모델 확인 wt(차체무게), qesc(드래그 레이스 타임), am(미션종류) df_stepCall: lm(formula = mpg ~ wt + qsec + am, data = df) Coefficients: (Intercept) wt qsec am 9.618 -3.917 1.226 2.936leaps 패키지 사용 - regsubsets()
install.packages('leaps')package 'leaps' successfully unpacked and MD5 sums checked The downloaded binary packages are in C:\Users\205\AppData\Local\Temp\Rtmpk3oBnd\downloaded_packageslibrary(leaps)Warning message: "package 'leaps' was built under R version 4.0.2"df <- mtcars# regsubsets() - BIC method='exhaustive' df_leaps <- regsubsets(mpg~., data=df , nvmax=10, method='exhaustive')# 결과 확인 # 각 변수 갯수별 변수를 뽑아줌 # 1개의 변수만 쓴다면 => wt # 2개의 변수만 쓴다면 => cyl, wt # 3개의 변수만 쓴다면 => wt, qsec(드래그타임, 느린차), am summary(df_leaps)Subset selection object Call: regsubsets.formula(mpg ~ ., data = df, nvmax = 10, method = "exhaustive") 10 Variables (and intercept) Forced in Forced out cyl FALSE FALSE disp FALSE FALSE hp FALSE FALSE drat FALSE FALSE wt FALSE FALSE qsec FALSE FALSE vs FALSE FALSE am FALSE FALSE gear FALSE FALSE carb FALSE FALSE 1 subsets of each size up to 10 Selection Algorithm: exhaustive cyl disp hp drat wt qsec vs am gear carb 1 ( 1 ) " " " " " " " " "*" " " " " " " " " " " 2 ( 1 ) "*" " " " " " " "*" " " " " " " " " " " 3 ( 1 ) " " " " " " " " "*" "*" " " "*" " " " " 4 ( 1 ) " " " " "*" " " "*" "*" " " "*" " " " " 5 ( 1 ) " " "*" "*" " " "*" "*" " " "*" " " " " 6 ( 1 ) " " "*" "*" "*" "*" "*" " " "*" " " " " 7 ( 1 ) " " "*" "*" "*" "*" "*" " " "*" "*" " " 8 ( 1 ) " " "*" "*" "*" "*" "*" " " "*" "*" "*" 9 ( 1 ) " " "*" "*" "*" "*" "*" "*" "*" "*" "*" 10 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"# BIC 값 확인으로 사용 모델 선택 - 변수 3개 선택 -46.7732016358928 BestBic <- summary(df_leaps)$bic BestBic- -37.7946153185172
- -46.348243336331
- -46.7732016358928
- -45.099468000674
- -42.9871333658026
- -40.2266298608964
- -37.0962985327756
- -33.7785850465411
- -30.3710226982818
- -26.9226107507162
# 그래프로 변수 찾기 Min.val <- which.min(BestBic) plot(BestBic, type='b') points(Min.val, BestBic[Min.val], cex=5, col='red', pch=20)
가장 낮은 값 확인 # 최적의 모델 찾기 coef coef(df_leaps, 3)- (Intercept)
- 9.61778051456159
- wt
- -3.91650372494249
- qsec
- 1.2258859715837
- am
- 2.93583719188942
전진선택법
# regsubsets() - BIC method='backward' df_leaps <- regsubsets(mpg~., data=df, nvmax=10, method='forward')# 결과 확인 # 처음에 선택된 변수는 계속 같이 다님 summary(df_leaps)Subset selection object Call: regsubsets.formula(mpg ~ ., data = df, nvmax = 10, method = "forward") 10 Variables (and intercept) Forced in Forced out cyl FALSE FALSE disp FALSE FALSE hp FALSE FALSE drat FALSE FALSE wt FALSE FALSE qsec FALSE FALSE vs FALSE FALSE am FALSE FALSE gear FALSE FALSE carb FALSE FALSE 1 subsets of each size up to 10 Selection Algorithm: forward cyl disp hp drat wt qsec vs am gear carb 1 ( 1 ) " " " " " " " " "*" " " " " " " " " " " 2 ( 1 ) "*" " " " " " " "*" " " " " " " " " " " 3 ( 1 ) "*" " " "*" " " "*" " " " " " " " " " " 4 ( 1 ) "*" " " "*" " " "*" " " " " "*" " " " " 5 ( 1 ) "*" " " "*" " " "*" "*" " " "*" " " " " 6 ( 1 ) "*" "*" "*" " " "*" "*" " " "*" " " " " 7 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" " " " " 8 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " 9 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" "*" 10 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"ForwardBic <- summary(df_leaps)$bic Min.val <- which.min(ForwardBic)plot(ForwardBic, type='b') points(Min.val, BestBic[Min.val], cex=5, col='red', pch=20)
전진선택법 일 때 가장 낮은 값 # 최적의 모델 구현 coef(df_leaps, 2)- (Intercept)
- 39.686261480253
- cyl
- -1.5077949682598
- wt
- -3.19097213898375
후진제거법
# regsubsets() - BIC method='backward' df_leaps <- regsubsets(mpg~., data=df, nvmax=10, method='backward')# 결과 확인 # 아래에서 위로 결과 확인 summary(df_leaps)Subset selection object Call: regsubsets.formula(mpg ~ ., data = df, nvmax = 10, method = "backward") 10 Variables (and intercept) Forced in Forced out cyl FALSE FALSE disp FALSE FALSE hp FALSE FALSE drat FALSE FALSE wt FALSE FALSE qsec FALSE FALSE vs FALSE FALSE am FALSE FALSE gear FALSE FALSE carb FALSE FALSE 1 subsets of each size up to 10 Selection Algorithm: backward cyl disp hp drat wt qsec vs am gear carb 1 ( 1 ) " " " " " " " " "*" " " " " " " " " " " 2 ( 1 ) " " " " " " " " "*" "*" " " " " " " " " 3 ( 1 ) " " " " " " " " "*" "*" " " "*" " " " " 4 ( 1 ) " " " " "*" " " "*" "*" " " "*" " " " " 5 ( 1 ) " " "*" "*" " " "*" "*" " " "*" " " " " 6 ( 1 ) " " "*" "*" "*" "*" "*" " " "*" " " " " 7 ( 1 ) " " "*" "*" "*" "*" "*" " " "*" "*" " " 8 ( 1 ) " " "*" "*" "*" "*" "*" " " "*" "*" "*" 9 ( 1 ) " " "*" "*" "*" "*" "*" "*" "*" "*" "*" 10 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"BackwardBic <- summary(df_leaps)$bic Min.val <- which.min(BackwardBic)plot(BackwardBic, type='b') points(Min.val, BackwardBic[Min.val], cex=5, col='red', pch=20)
후진제거법 일 떄 가장 작은 값 # 최적의 모델 구현 coef(df_leaps, 3)- (Intercept)
- 9.61778051456161
- wt
- -3.91650372494249
- qsec
- 1.2258859715837
- am
- 2.93583719188942
명목형 변수 해석하기
-
문자형 -> 숫자형
-
없다 0, 있다1 바꾸어서 의미를 파악
-
남자 0, 여자 1 y = 2 + 4x => 남자라면 2, 여자면 6이됨
head(mtcars)mpg cyl disp hp drat wt qsec vs am gear carb <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1 Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1 Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2 Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1 # am 0 auto, 1 수동 => 수동이면 연비가 올라감 7.245 lm(mpg ~ am, data = mtcars)Call: lm(formula = mpg ~ am, data = mtcars) Coefficients: (Intercept) am 17.147 7.245다중 명목형 변수
install.packages('car')also installing the dependencies 'matrixStats', 'RcppArmadillo', 'zip', 'SparseM', 'MatrixModels', 'conquer', 'sp', 'openxlsx', 'minqa', 'nloptr', 'statmod', 'RcppEigen', 'carData', 'abind', 'pbkrtest', 'quantreg', 'maptools', 'rio', 'lme4' package 'matrixStats' successfully unpacked and MD5 sums checked package 'RcppArmadillo' successfully unpacked and MD5 sums checked package 'zip' successfully unpacked and MD5 sums checked package 'SparseM' successfully unpacked and MD5 sums checked package 'MatrixModels' successfully unpacked and MD5 sums checked package 'conquer' successfully unpacked and MD5 sums checked package 'sp' successfully unpacked and MD5 sums checked package 'openxlsx' successfully unpacked and MD5 sums checked package 'minqa' successfully unpacked and MD5 sums checked package 'nloptr' successfully unpacked and MD5 sums checked package 'statmod' successfully unpacked and MD5 sums checked package 'RcppEigen' successfully unpacked and MD5 sums checked package 'carData' successfully unpacked and MD5 sums checked package 'abind' successfully unpacked and MD5 sums checked package 'pbkrtest' successfully unpacked and MD5 sums checked package 'quantreg' successfully unpacked and MD5 sums checked package 'maptools' successfully unpacked and MD5 sums checked package 'rio' successfully unpacked and MD5 sums checked package 'lme4' successfully unpacked and MD5 sums checked package 'car' successfully unpacked and MD5 sums checked The downloaded binary packages are in C:\Users\205\AppData\Local\Temp\Rtmpk3oBnd\downloaded_packageslibrary(car)Warning message: "package 'car' was built under R version 4.0.2" Loading required package: carDatahead(Vocab, 3)year sex education vocabulary <dbl> <fct> <dbl> <dbl> 19740001 1974 Male 14 9 19740002 1974 Male 16 9 19740003 1974 Female 10 9 str(Vocab)'data.frame': 30351 obs. of 4 variables: $ year : num 1974 1974 1974 1974 1974 ... $ sex : Factor w/ 2 levels "Female","Male": 2 2 1 1 1 2 2 2 1 1 ... $ education : num 14 16 10 10 12 16 17 10 12 11 ... $ vocabulary: num 9 9 9 5 8 8 9 5 3 5 ... - attr(*, "na.action")= 'omit' Named int [1:32115] 1 2 3 4 5 6 7 8 9 10 ... ..- attr(*, "names")= chr [1:32115] "19720001" "19720002" "19720003" "19720004" ...# year 관측연도, sex 성별, education 교육횟수, vocabulary 단어시험점수 summary(Vocab)year sex education vocabulary Min. :1974 Female:17148 Min. : 0.00 Min. : 0.000 1st Qu.:1987 Male :13203 1st Qu.:12.00 1st Qu.: 5.000 Median :1994 Median :12.00 Median : 6.000 Mean :1995 Mean :13.03 Mean : 6.004 3rd Qu.:2006 3rd Qu.:15.00 3rd Qu.: 7.000 Max. :2016 Max. :20.00 Max. :10.000?VocabLm <- lm(Vocab$vocabulary~Vocab$sex+Vocab$education, data = Vocab) LmCall: lm(formula = Vocab$vocabulary ~ Vocab$sex + Vocab$education, data = Vocab) Coefficients: (Intercept) Vocab$sexMale Vocab$education 1.7366 -0.1687 0.3330Vocab$sexMale 남자이면 점수 -0.1687 낮아짐
교육 1번에 0.333점 올라감
-