SVM

머신러닝

서포트 벡터 머신(SVM) - Support Vector Machine

• 다양한 연구를 통해 굉장히 높은 인식 성능 발휘

• 선을 구성하는 매개변수를 조정해서 요소의 구분선을 찾고 이른 기반으로 패턴 인식

• 주어진 데이터가 어느 카테고리에 속할지 판단하는 이진 선형 분류 모델

서포트 벡터 머신(SVM) 개념

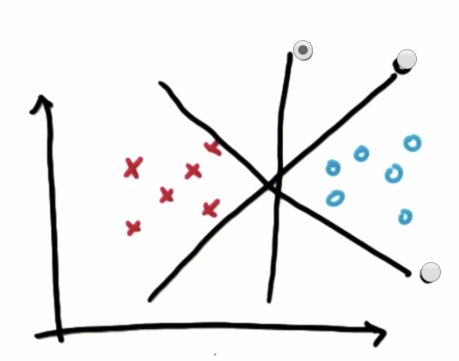
출처: Udacity

빨간 X와 파란 O 구분하는 선중 두 데이터를 잘 구분한 선은?

Margin의 최대화

출처: Udacity

• 가운데 선이 Margin을 최대화

• Margin은 선과 가장 가까운 양 옆 데이터와의 거리

• 서포트 백터(Support) : 선과 가장 가까운 포인트

• Margin은 선과 서포트 벡터와의 거리

• Descision Boundary : 데이터 구분하는 선

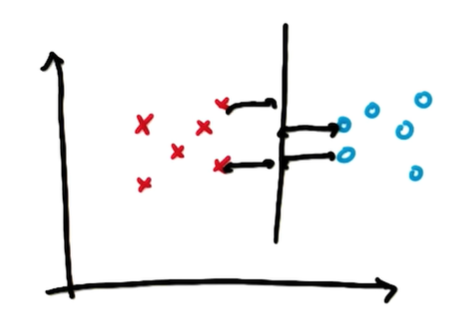
Robustness

출처: Udacity

• 양 옆 서포트 벡터와의 Margin을 최대화하면 robustness도 최대화

• 데이터 과학에서 로버스트(robust)

  • 아웃라이어(outlier)의 영향을 받지 않는다는 뜻

• 평균은 로버스트(robust)하지 않다고 하고, 중앙값은 로버스트(robust)하다

데이터의 정확한 분류

출처: Udacity

둘 중 어떤 선이 SVM의 구분선으로 적절할까요?

• 첫 번째 구분선이 Margin이 더 큼

• 하지만 첫 번째 구분선은 데이터를 정확히 구분하지 못함

• 데이터를 정확히 분류하는 범위를 먼저 찾고, 그 범위 안에서 Margin을 최대화하는 구분선을 택하는 것

Outlier(이상값) 처리

출처: Udacity

• SVM은 우선 두 데이터를 정확히 구분하는 선을 찾음

• 두 데이터를 정확히 구분하는 직선은 없음

• 어느 정도 outlier를 무시하고 최적의 구분선을 찾음

• 빨간 포인트 사이에 섞인 파란 포인트는 outlier로 취급

• outlier는 무시하고 Margin을 최대화하는 구분선을 찾음

커널 트릭 (Kernel Trick)

• 저차원 공간(low dimensional space)을 고차원 공간(high dimensional space)으로 매핑해주는 작업

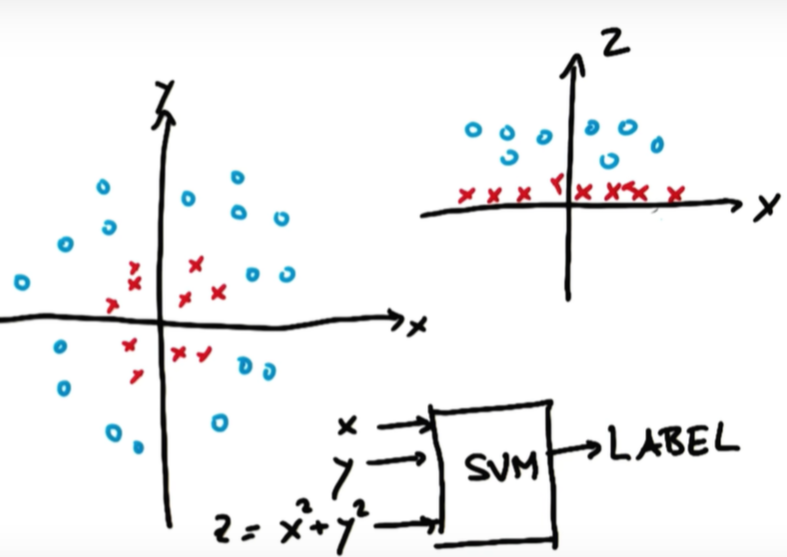
출처: Udacity

• 빨간 포인트와 파란 포인트를 구분할 수 있는 linear line은 없음

• 차원을 바꿔주어 구분선을 그림

• z = x^2 + y^2

• 빨간 포인트는 원점으로부터의 거리가 짧아 z가 작음

• 파란 포인트는 원점으로부터의 거리가 길어 z가 큼

출처: Udacity

• 오른쪽 그래프에서 linear하게 그린 구분선은 왼쪽에서 원형으로 된 구분선과 동일

• 차원이 달라져서 구분선의 모양이 다른 것뿐

• 저차원 공간(low dimensional space)을 고차원 공간(high dimensional space)으로 매핑해주는 작업

• 처음부터 저차원 공간에서 non linear separable line을 구하려면 쉽지 않음

• 고차원 linear를 구하고 저차원의 non linear한 해를 구한 것

sklearn SVM Parameter

Kernel parameter

• linear, polynomial, sigmoid, rbf 등의 kernel을 선택 가능

• 디폴트는 rbf

• decision boundary의 모양을 선형으로 할지 다항식형으로 할지 등을 결정

  kernel = linear 인 SVM은 어떤 것일까요?

출처: Udacity

C

• Controls tradeoff detween smooth decision boundary and classfying training points correctly

출처: Udacity

• 초록색 구분선은 C가 큰 decision boundary

• 주황색 구분선은 C가 작은 decision boundary

• C가 크면 training 포인트를 정확히 구분

• C가 작으면 smooth한 decision boundary

• C가 크면 decision boundary는 더 굴곡짐

• C가 작으면 decision boundary는 직선에 가까움

Gamma(γ)

• Gamma: Defines how far the influence of a single training point reaches

• reach는 decision boudary의 굴곡에 영향을 주는 데이터의 범위

• Gamma가 작다면 reach가 멀다는 뜻

• Gamma가 크다면 reach가 좁다는 뜻

Gamma 값이 클 때

• Gamma가 크면 decision boundary는 더 굴곡짐

출처: Udacity

• Gammar 값이 크다는 것은 위와 같이 reach가 좁다는 뜻

• reach가 좁기 때문에 원형 안에 있는 포인트는 decision boundary에 영향을 주지 않음

• 가까이 있는 포인트들만이 선의 굴곡에 영향

• decision boundary는 굴곡지게됨

• 멀리 있는 포인트는 영향이 없으므로 선과 가까이 있는 포인트 하나하나의 영향이 상대적으로 크기 때문

출처: Udacity

Gamma 값이 작을 때

• Gamma가 작으면 decision boundary는 직선에 가까움

출처: Udacity

• decision boundary와 가까이 있는 포인트 하나하나가 decision boundary에 주는 영향이 상대적으로 작음

• 그래서 선이 포인트 하나 때문에 구부러지지 않음

C 와 Gamma

• 값이 커짐에 따라 C는 두 데이터를 정확히 구분하는 것에 초점

• Gamma는 개별 데이터마다 decision boundary를 만드는 것에 초점

• C는 아무리 커져도 outlier가 없다면 decision boudnary는 하나

• Gamma는 커짐에 따라 여러 decision boundary

출처: Udacity

오버피팅 (과적합, Overfitting)

출처: Udacity

• 오버피팅이란 훈련 데이터를 지나치게 학습하는 것

• 훈련 데이터에서는 100%에 가까운 성능을 내지만 테스트 데이터에서는 성능이 굉장히 떨어짐

• Kerenl, C, Gamma 모두 오버피팅에 영향을 줄 수 있는 파라미터

• 머신러닝에서도 성능을 높히는 것과 오버피팅을 막는 것 사이의 균형을 잘 지켜야 함

• SVM은 training time이 길기 때문에 사이즈가 큰 데이터 셋에는 부적합

• 노이즈가 많은 데이터 셋에서는 오버피팅이 될 수 있어 부적합

---

컴퓨터에게 비만 학습시키기

• 비만도 계산 BMI => 저체중, 정상, 비만 레이블

• BMI = <몸무게 kg> / 키(m)**2

데이터셋

• 20000개의 저체중(thin), 정상(normal), 비만(fat) 데이터 생산

import random

# BMI를 계산해서 레이블을 리턴하는 함수
def calc_bmi(h, w):
    bmi = w / (h/100) ** 2
    if bmi < 18.5: return 'thin'
    if bmi <25: return 'normal'
    return 'fat'

# 출력 파일 준비하기
fp = open('bmi.csv', 'w', encoding='utf-8')
fp.write('height,weight,label\r\n') # 공백주의! 공백 넣지말것

# 무작위로 데이터 생성하기
cnt = {'thin':0, 'normal':0, 'fat':0}
for i in range(20000):
    h = random.randint(120, 200)
    w = random.randint(35, 80)
    label = calc_bmi(h, w)
    cnt[label] += 1
    fp.write('{0},{1},{2}\r\n'.format(h , w, label))
fp.close()
print('ok', cnt)

ok {'thin': 6459, 'normal': 5827, 'fat': 7714}

학습 및 테스트

from sklearn import svm, metrics
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import pandas as pd

# 키와 몸무게 데이터 읽어 들이기 --- (1)
tbl = pd.read_csv('bmi.csv')

tbl.head()

	height	weight	label
0	170	78	fat
1	181	46	thin
2	178	54	thin
3	190	70	normal
4	159	59	normal

# 칼럼(열)을 자르고 정규화하기 --- (2)
label = tbl["label"]

w = tbl["weight"] / 100 # 최대 100kg라고 가정
h = tbl["height"] / 200 # 최대 200cm라고 가정
wh = pd.concat([w, h], axis=1)

label.head()

0       fat
1      thin
2      thin
3    normal
4    normal
Name: label, dtype: object

wh.head()

	weight	height
0	0.78	0.850
1	0.46	0.905
2	0.54	0.890
3	0.70	0.950
4	0.59	0.795

# 학습 전용 데이터와 테스트 전용 데이터로 나누기 --- (3)
data_train, data_test, label_train, label_test = train_test_split(wh, label)

# 데이터 학습하기 --- (4)
clf = svm.SVC()
clf.fit(data_train, label_train)

SVC()

# 데이터 예측하기 --- (5)
predict = clf.predict(data_test)

# 결과 테스트 하기 --- (6)
ac_score = metrics.accuracy_score(label_test, predict)
cl_report = metrics.classification_report(label_test, predict)
print("정답률 =", ac_score)
print("리포트 =\n", cl_report)

정답률 = 0.995
리포트 =
               precision    recall  f1-score   support

         fat       1.00      0.99      1.00      1915
      normal       0.98      1.00      0.99      1458
        thin       1.00      0.99      1.00      1627

    accuracy                           0.99      5000
   macro avg       0.99      1.00      0.99      5000
weighted avg       1.00      0.99      1.00      5000

데이터 분포 확인하기

# Pandas로 CSV 파일 읽어 들이기
tbl = pd.read_csv('bmi.csv', index_col = 2)

# 그래프 그리기 시작
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)

# 서프 플롯 전용 - 지정한 레이블을 임의의 색으로 칠하기
def scatter(lbl, color):
    b = tbl.loc[lbl]
    ax.scatter(b['weight'], b['height'], c=color, label=lbl)
scatter('fat', 'red')
scatter('normal', 'yellow')
scatter('thin', 'purple')
ax.legend()

# plt.savefig("bmi-test.png")
plt.show()

LinearSVC()

• 선형 커널에 특화 되있으며 계산이 빠름

# 키와 몸무게 데이터 읽어 들이기 --- (1)
tbl = pd.read_csv('bmi.csv')

# 칼럼(열)을 자르고 정규화하기 --- (2)
label = tbl['label']
w = tbl["weight"] / 100 # 최대 100kg라고 가정
h = tbl["height"] / 200 # 최대 200cm라고 가정
wh = pd.concat([w, h], axis=1)

# 학습 전용 데이터와 테스트 전용 데이터로 나누기 --- (3)
data_train, data_test, label_train, label_test = train_test_split(wh, label)

# 데이터 학습하기 --- (4)
clf = svm.LinearSVC()
clf.fit(data_train, label_train)

# 데이터 예측하기 --- (5)
predict = clf.predict(data_test)

# 결과 테스트하기 --- (6)
ac_score = metrics.accuracy_score(label_test, predict)
cl_report = metrics.classification_report(label_test, predict)
print("정답률 =", ac_score)
print("리포트 =\n", cl_report)

정답률 = 0.924
리포트 =
               precision    recall  f1-score   support

         fat       0.91      1.00      0.95      1942
      normal       1.00      0.74      0.85      1431
        thin       0.90      1.00      0.94      1627

    accuracy                           0.92      5000
   macro avg       0.93      0.91      0.92      5000
weighted avg       0.93      0.92      0.92      5000

서포트 벡터 머신(SVM) 개념

• https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-2%EC%84%9C%ED%8F%AC%ED%8A%B8-%EB%B2%A1%ED%84%B0-%EB%A8%B8%EC%8B%A0-SVM?category=1057680

• https://datascienceschool.net/view-notebook/6c6d450cb2ee49558856fd924b326e00/